知识图谱与机器学习 | KG入门 -- Part1-b 图深度学习
图深入学习越来越重要。在这里,我将使用Spektral库和平台MatrixDS展示关于图的机器学习和深度学习的基本思想。

编译|Arno
来源|Medium
说明:这是上一篇文章的延续,主要强调深度学习。
介绍

我们正在定义一种新的机器学习方法,专注于一种新的范式 -- Data Fabric。
在上一篇文章中,我们对机器学习给出了新的定义:
机器学习是一种自动发现Data Fabric中隐藏的洞察(insight)的过程,它使用的算法能够发现这些洞察(insight),而无需专门为此编写程序,从而创建模型来解决特定(或多个)问题。
理解这一点的前提是我们创建了一个Data Fabric。对我来说,最好的工具就是Anzo,正如我之前提到的。
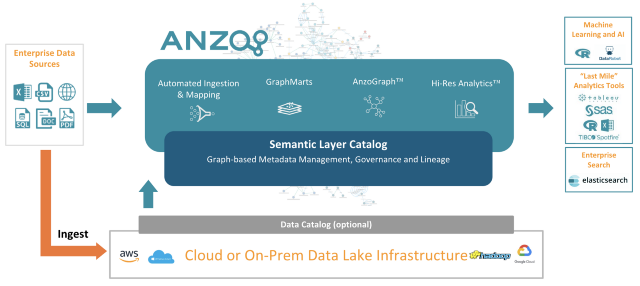
你可以使用Anzo构建所谓的“企业知识图谱”,当然也创建了Data Fabric。
但现在我想集中讲一个机器学习的主题--深度学习。这里我给出了深度学习的定义:
深度学习是机器学习的一个特定子领域,是一种从数据中学习表示的新方法,强调学习越来越有意义的表示的连续“层”(神经网络)。
在这里,我们将讨论深度学习和图论的结合,看看它如何帮助向前推进我们的研究。
目标
建立对Data Fabric进行深度学习的基础。
细节
- 描述图深度学习的基础
- 探索Spektral库
- 验证对Data Fabric进行深度学习的可能性。
主要的假设
如果我们能够创建一个支持公司所有数据的Data Fabric,那么通过使用神经网络(深度学习)从数据中学习越来越有意义的表示来发现洞察(insight)的自动过程就可以在Data Fabric中运行。
第一节 图深度学习
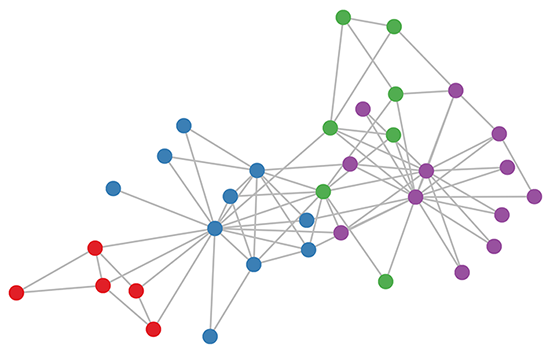
通常我们用张量来建立神经网络,但是记住我们也可以用矩阵来定义张量,图也可以通过矩阵来定义。
Spektral库的文档中声明图一般由三个矩阵表示:
- A $\in ${0,1} ^ {N$ \times $N}:一种二值邻接矩阵,如果节点i与j之间有连接,则$A_{ij}$=1,否则$A_{ij}$=0;
- X $\in$ R ^ (N$\times$F): 编码节点属性(或特征)的矩阵,其中F维属性向量与每个节点相关联;
- E $\in$ R ^ (N$\times$N$\times$S):一种编码边属性的矩阵,其中一个s维属性向量与每个边相关联。
我不会在这里详细介绍,但如果你想更全面地了解图上的深度学习,请查看Tobias Skovgaard Jepsen的文章:
https://towardsdatascience.com/how-to-do-deep-learning-on-graphs-with-graph-convolutional-networks-7d2250723780
这里的重要部分是图神经网络(GNN)的概念。
图神经网络(GNN)

GNN的思想很简单:为了对图的结构信息进行编码,每个节点$v_i$可以表示为一个低维状态向量$s_i$, 1≤i≤N(记住向量可以看作秩为1的张量,张量可以用矩阵表示)。
学习图深度模型的任务大致可以分为两个领域: - 关注节点的任务:这些任务与图中的各个节点相关联。比如节点分类、链接预测和节点推荐。 - 关注图的任务:这些任务与整个图相关联。比如图分类、估计图的某些性质或生成图。
第二节 使用Spektral进行深度学习

Spektral作者将Spektral定义为关系表示学习的框架,用Python构建并基于Keras API。
安装
我们将使用MatrixDS作为工具或运行我们的代码。记住,除了Anzo,你也可以在这里运行这个代码。
你需要做的第一件事是复制MatrixDS项目:
https://community.platform.matrixds.com/community/project/5c6ae7c8c1b06ba1e18f2a6e/files
通过点击:
 你将安装库并使一切正常工作。
你将安装库并使一切正常工作。
如果你在外面运行这个,记住这个框架是在Ubuntu 16.04和18.04上测试的,你应该安装:
sudo apt install graphviz libgraphviz-dev libcgraph6
然后安装库:
pip install spektral
数据表示
在Spektral中,一些层和函数被实现以在一个图上工作,而另一些则考虑图形的集合。
该框架有以下三种主要的操作模式: - single,这种模式下我们考虑单个图,它的拓扑和属性; - batch,这种模式下我们考虑一组图,每个图都有自己的拓扑结构和属性; - mixed,这种模式下我们考虑一个具有固定拓扑结构,但具有不同属性的集合的图;这可以看作是批处理模式特殊情况(即所有邻接矩阵都是相同的),但由于计算原因而单独处理。
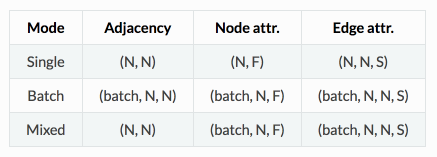
例如,如果我们运行
from spektral.datasets import citation
adj, node_features, edge_features, _, _, _, _, _ = citation.load_data('cora')
我们将在sigle模式下加载数据,我们的邻接矩阵为:
In [3]: adj.shape
Out[3]: (2708, 2708)
节点属性为:
In [3]: node_attributes.shape
Out[3]: (2708, 2708)
边属性为:
In [3]: edge_attributes.shape
Out[3]: (2708, 7)
使用图注意层(GAT)进行半监督分类
这里假设你知道Keras,对于更多的细节和代码可以查看:
https://community.platform.matrixds.com/community/project/5c6ae7c8c1b06ba1e18f2a6e/files
GAT是一种新型的神经网络结构,它利用掩蔽的自注意层对图形结构数据进行操作。在Spektral中,GraphAttention层计算卷积与layers.GraphConv类似,但是使用注意机制来加权邻接矩阵,而不是使用归一化拉普拉斯。
它们的工作方式是通过堆叠节点能够参与其邻域特征的层,这使得(隐式)为邻域中的不同节点指定不同的权重,而不需要任何开销过大的矩阵操作(例如矩阵求逆)或是需要事先了解图形结构。
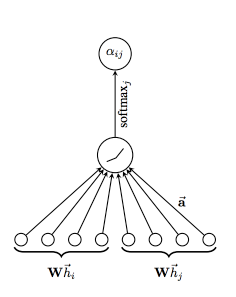
我们将使用的模型非常简单:
# Layers
dropout_1 = Dropout(dropout_rate)(X_in)
graph_attention_1 = GraphAttention(gat_channels,
attn_heads=n_attn_heads,
attn_heads_reduction='concat',
dropout_rate=dropout_rate,
activation='elu',
kernel_regularizer=l2(l2_reg),
attn_kernel_regularizer=l2(l2_reg))([dropout_1, A_in])
dropout_2 = Dropout(dropout_rate)(graph_attention_1)
graph_attention_2 = GraphAttention(n_classes,
attn_heads=1,
attn_heads_reduction='average',
dropout_rate=dropout_rate,
activation='softmax',
kernel_regularizer=l2(l2_reg),
attn_kernel_regularizer=l2(l2_reg))([dropout_2, A_in])
# Build model
model = Model(inputs=[X_in, A_in], outputs=graph_attention_2)
optimizer = Adam(lr=learning_rate)
model.compile(optimizer=optimizer,
loss='categorical_crossentropy',
weighted_metrics=['acc'])
model.summary()
# Callbacks
es_callback = EarlyStopping(monitor='val_weighted_acc', patience=es_patience)
tb_callback = TensorBoard(log_dir=log_dir, batch_size=N)
mc_callback = ModelCheckpoint(log_dir + 'best_model.h5',
monitor='val_weighted_acc',
save_best_only=True,
save_weights_only=True)
但是这个模型会很大:
__________________________________________________________________________________________________
Layer (type) Output Shape Param # Connected to
==================================================================================================
input_1 (InputLayer) (None, 1433) 0
__________________________________________________________________________________________________
dropout_1 (Dropout) (None, 1433) 0 input_1[0][0]
__________________________________________________________________________________________________
input_2 (InputLayer) (None, 2708) 0
__________________________________________________________________________________________________
graph_attention_1 (GraphAttenti (None, 64) 91904 dropout_1[0][0]
input_2[0][0]
__________________________________________________________________________________________________
dropout_18 (Dropout) (None, 64) 0 graph_attention_1[0][0]
__________________________________________________________________________________________________
graph_attention_2 (GraphAttenti (None, 7) 469 dropout_18[0][0]
input_2[0][0]
==================================================================================================
Total params: 92,373
Trainable params: 92,373
Non-trainable params: 0
所以如果机器性能没有那么好的话,可以减少epochs的次数。 然后我们训练它(如果机器性能不够好,这可能需要几个小时):
# Train model
validation_data = ([node_features, adj], y_val, val_mask)
model.fit([node_features, adj],
y_train,
sample_weight=train_mask,
epochs=epochs,
batch_size=N,
validation_data=validation_data,
shuffle=False, # Shuffling data means shuffling the whole graph
callbacks=[es_callback, tb_callback, mc_callback])
得到最好的模型:
model.load_weights(log_dir + 'best_model.h5')
评估模型:
print('Evaluating model.')
eval_results = model.evaluate([node_features, adj],
y_test,
sample_weight=test_mask,
batch_size=N)
print('Done.\n'
'Test loss: {}\n'
'Test accuracy: {}'.format(*eval_results))
更多的信息可以参见MatrixDS项目:
https://community.platform.matrixds.com/community/project/5c6ae7c8c1b06ba1e18f2a6e/files
第三节 这在Data Fabric中处于什么位置?
如果你还记得上一部分,假设我们有一个Data Fabric:

一种洞察(insight)可以被认为是它的一个凹痕:

如果你在MatrixDS平台上使用本教程,你会发现我们使用的数据并不是一个简单的CS,但是我们为这个库提供了: - 一个N×N的邻接矩阵(N是节点数) - 一个N×D的特征矩阵(D是每个节点的特征数) - 一个N×E的二值标签矩阵(E是类的数量)
并且存储的是一系列文件:
ind.dataset_str.x => the feature vectors of the training instances as scipy.sparse.csr.csr_matrix object; ind.dataset_str.tx => the feature vectors of the test instances as scipy.sparse.csr.csr_matrix object; ind.dataset_str.allx => the feature vectors of both labeled and unlabeled training instances (a superset of ind.dataset_str.x) as scipy.sparse.csr.csr_matrix object; ind.dataset_str.y => the one-hot labels of the labeled training instances as numpy.ndarray object; ind.dataset_str.ty => the one-hot labels of the test instances as numpy.ndarray object; ind.dataset_str.ally => the labels for instances in ind.dataset_str.allx as numpy.ndarray object; ind.dataset_str.graph => a dict in the format {index: [index_of_neighbor_nodes]} as collections.defaultdict object; ind.dataset_str.test.index => the indices of test instances in graph, for the inductive setting as list object.
这些数据在图中,我们所做的就是把数据加载到库中。实际上,可以将数据转换为库中的NetworkX,numpy和sdf格式。
这意味着,如果我们将数据存储在一个Data Fabric中,我们就有了我们的知识图谱,因此我们已经有了很多这些特征,我们要做的就是找到一种方法,把它与库连接起来。这是现在最棘手的部分。
然后我们通过对Data Fabric内部的图运行深度学习算法的过程,开始在Data Fabric中寻找洞察(insight)。
这里有趣的部分是,可能有一些方法可以在图中运行这些算法,为了实现这一点,我们需要能够使用存储在图形结构中的固有数据来构建模型,Lauren Shin 的Neo4j有一个非常有趣的方法:
https://towardsdatascience.com/graphs-and-ml-multiple-linear-regression-c6920a1f2e70
但这项工作仍在进行中。我想象这个过程是这样的:
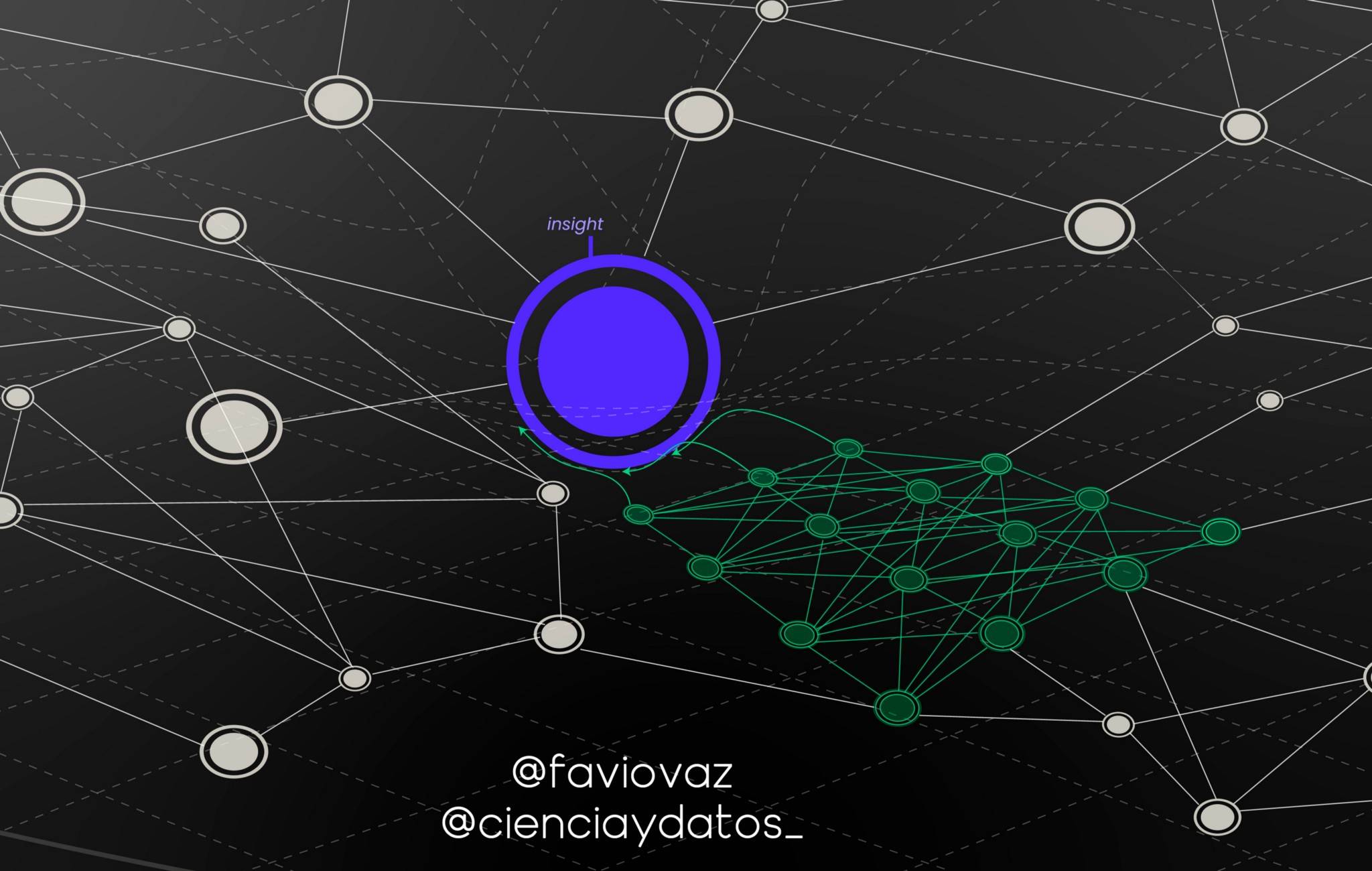
这意味着神经网络可以存在于Data Fabric中,而算法将与其中的资源一起运行。
我在这里甚至没有提到非欧几里德数据的概念,但之后的文章我们会讲到。
总结
如果能够将知识图谱与Spektral(或其他)库连接起来,则可以通过为已有的图数据部署图神经网络模型,在Data Fabric上运行深度学习算法。
除了标准图形推理等任务,像节点或图分类,基于图的深度学习的方法也被应用于广泛的学科,如建模社会影响,推荐系统,化学,物理,疾病或药物预测,自然语言处理(NLP),计算机视觉,交通预测和解决基于图的NP问题。可以参见
https://arxiv.org/pdf/1812.04202.pdf。